Vector Eigen, Eigen Valor 3x3 Matrix Calculator

 
Regular Matrix A =
Scalar Matrix (Z=c×I)
|A| =
Singular Matrix (A - c×I) =
|A - c×I| =
Trace of A =
Eigenvalue of c3 =
+ i
 
Eigenvalue of c2 =
+ i
Eigenvalue of c1 =
+ i
c3 in Eigenvector (x,y,z) values =
c2 in Eigenvector (x,y,z) values =
c1 in Eigenvector (x,y,z) values =

Um eigenvector de uma matriz quadrada A é um vector não zero v que, quando a matriz é multiplicada por V, produz um múltiplo constante de V, o multiplicador sendo comumente denotado por λ. Isto é: a v = λ v

(Porque essa equação usa pós-multiplicação por V, descreve um eigenvector direito.) O número λ é chamado de autovalor de um correspondente a v.

Todos os autovalores e eigenvectors satisfazem a equação AX = λx para uma determinada matriz quadrada A.

Calculadora de matriz simples para calcular o valor de Eigen e o vetor de Eigen de uma matriz 3x3. Digite os valores da matriz 3x3 e clique no botão Calcular.

Vestígio

O traço, tr (a) de uma matriz quadrada A é a soma de suas entradas diagonais. Enquanto a multiplicação matricial não é comutativa como mencionado acima, o traço do produto de duas matrizes é independente da ordem dos fatores:

tr (ab) = tr (ba).

Isto é imediato da definição de multiplicação matricial:

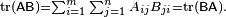
Além disso, o traço de uma matriz é igual à da sua transposição, ou seja,

tr (a) = tr (um t ).

Vector Eigen, Eigen Valor 3x3 Matrix Calculator
Calculadoras de recomendação Resolver desigualdades lineares Calculadora de distribuição hipergeométrica Calculadora de equação sexta Calculadora científica online. Efeito da calculadora de tamanho Equações de Transposição Resolvendo a calculadora Sinal para a calculadora de relação de ruído Calculadora do produto Cruz do vetor Calculadora de adição de vetor Calculadora de convolução online. Soma de calculadora consecutiva cubos Soma de calculadora de praças Soma de calculadora de quadrados consecutivos Calculadora de conjuntos de diferença simétrica Calculadora de teorema binômio