Eigenvectors e Cálculo de Eigenvalues |
Um eigenvector de uma matriz quadrada A é um vector não zero v, quando um v = λ V, o λ é chamado de autovalor de um correspondente a v.
Todos os autovalores e eigenvectors satisfazem a equação AX = λx para uma determinada matriz quadrada A.
Os autovetores on-line e a calculadora de eigenvalues podem obter | A |, matriz singular (A - C × i), traço de um valor de Eigen da matriz A
Por exemplo
Para matriz.
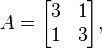
o vetor
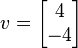
é um eigenvector com a autovalue 2.
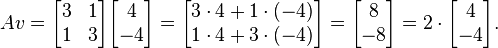
Por outro lado o vetor
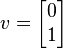
é não um eigenvector, já
- .
- .
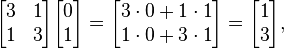
E este vector não é um múltiplo do vetor original v.
seleção de idioma:日本語 | 한국어 | Français | Español | ไทย| عربي | русский язык | Português | Deutsch| Italiano | Ελληνικά | Nederlands | Polskie| Tiếng Việt| বাংলা| Indonesia| Pilipino| Türk| فارسی| ລາວ| ဗမာ| български| Català| čeština| Қазақ| Magyar| Română| Україна
Copyright ©2021 - 2031 All Rights Reserved.